Rで中心極限定理を感じる (apply, matrix, matplot)

前回、コイン投げを繰り返すと表が出る確率（相対頻度）は、真の確率50％に近づいてゆくと書きました。今回は、コイン投げを繰り返すとき、真の確率からのずれはどのような分布になるかを考えます。

目次

1. 誤差
2. matrix、apply
3. 誤差の分布

*  *  *

1　誤差

歪みのないコイン投げて表が出る確率は50％です。しかし、前回書いたコードを繰り返し実行すると、コインを700回投げて表が出る確率は、毎回50％より少し高かったり低かったりします。毎回の試行で生じる真の値からのずれを誤差といいます。

700回のコイン投げを100ラウンド繰り返すと、数十ラウンドは確率が50％より高くなり、残りの数十ラウンドは確率が50％より低くなります。値がこのようにばらつくことを「誤差が分布する」といいます。分布とは、値がばらつくようすのことです。

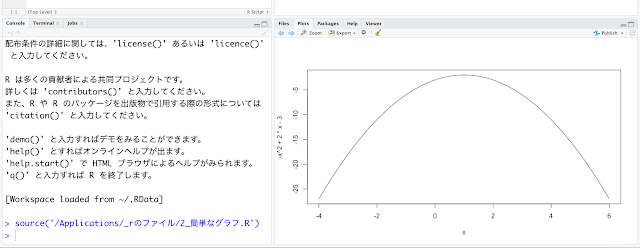
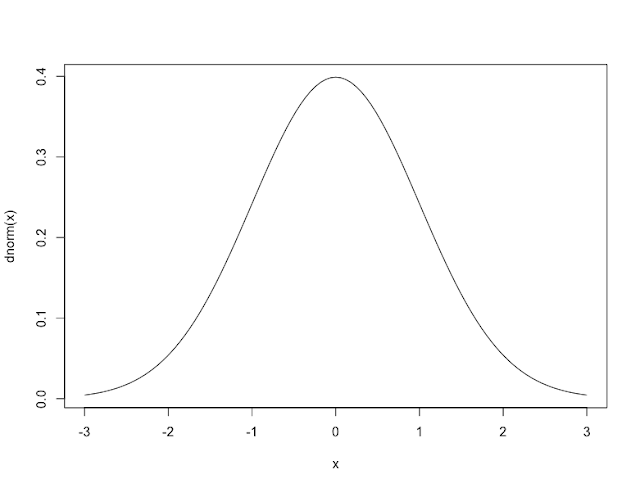
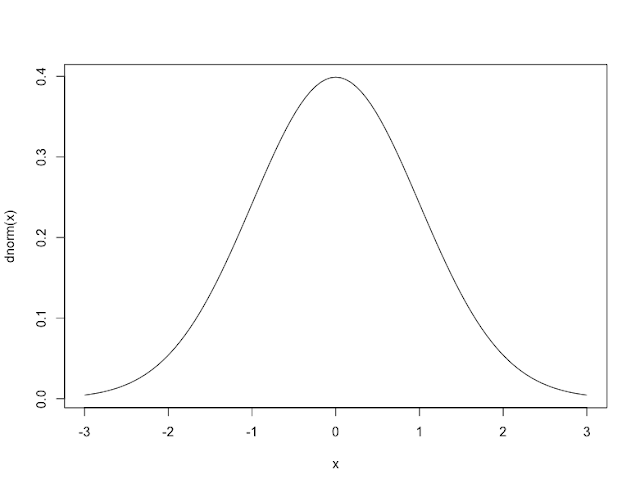
ド・モアブルという人は、毎回のラウンドでコインを投げる回数が十分多ければ、誤差が正規分布することを発見しました。後にラプラスという人が考えを拡張しましたので、ド・モアブル＝ラプラスの定理といいます。正規分布は、下図のように真ん中が高く、両端が低いつりがね状の分布です。どこかで一度はみたことがあるのではないでしょうか。



















ガウスという人は、コイン投げだけではなく、ほかの現象の誤差もおしなべて正規分布するとして、誤差の理論を体系化しました。それで、正規分布をガウス分布ともいいます。

誤差には公理とよばれるものが3つあります。

・小さい誤差は大きい誤差より多く観察される（単峰性）
・プラスの誤差とマイナスの誤差の起こりやすさは等しい（対称性）
・とても大きい誤差はほとんど観察されない（外れ値）

正規分布は、これら3つの条件をよく満たす特別な分布です。それで統計学に繰り返し登場します。何年か前に『統計学が最強の学問である』という本がベストセラーになりました。「統計学は誤差の科学である」と言ったほうが、専門家は喜ぶかもしれません。

*  *  *

2　matrix、apply

コードを効率よく書くのに、行列はとても便利です。プログラミングで行列とは、エクセルの表をコードにしたものと思ってください。数のならびを行列にしておくと、繰り返し作業がかんたんにできます。

たとえば、コードを次のように書くと、コインを3回投げる試行を2ラウンド行った結果を2行3列の表にできます。1行目は前回説明したコイン投げの命令文です。2行目はコイン投げの結果をつづら折りにして2行3列の表に格納する命令文です。

toss=sample(x=c(0,1), size=2*3, replace=TRUE)
toss=matrix(toss, nrow=2, ncol=3)

たとえば、{1, 1, 1, 0, 0, 1} というコイン投げの結果は

1, 1, 0
1, 0, 1

と折り込まれます。列に方向に3回折り込む感じです。つづいて、折り込んだコイン投げの結果を行方向に足しあげ、各回までの確率を計算します。コードを次のように書くとこの作業ができます。1行目は作成した toss という名前の行列を1行ごとに足し上げる命令文です。apply は、これまで数列に利用してきた cumsum という関数を行列に適用するためのものです。第2要素の 1 は行別に足し上げる指定です。

toss=apply(toss, 1, cumsum)

上の行列を行別に足し上げると次のようになります。

1行目　1, 2, 2
2行目　1, 1, 2

さらに、次の命令文で、足しあげた数を足し上げる回数で割ります。

toss=toss/(1:3)

(1:3) は {1, 2, 3} です。これで1行目、2行目の結果を割ると

1行目　1,   1, 0.6666
2行目　1, 0.5, 0.6666

となります。前回、700回コインを投げる試行を1度だけやりました。今回それを拡張して、n 回コインを投げる試行を r 回繰り返します。matrix と apply を使えば、複合的な試行を繰り返すコードをかんたんに書くことができます。

*  *  *

3　誤差の分布

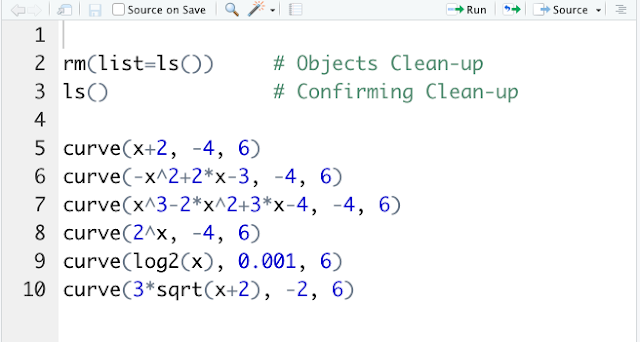
誤差が正規分布するかRで検証しましょう。下図のコードを入力して実行してみてください。これくらいの長さのコードが数回つづいていますので、だんだん入力に慣れてきたのではないでしょうか。

















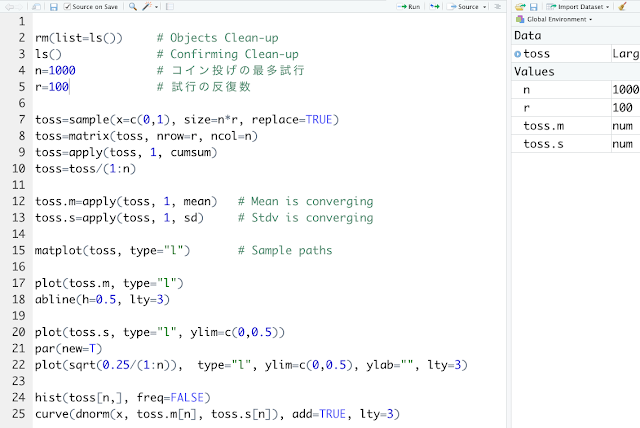
うまくいけば、右下の領域に次のような4枚のグラフがあらわれます。なかなか壮観ですね（ここでは一覧性を高めるために4つまとめて表示していますが、上のコードでは4枚別々のグラフになります。）

（par(mfrow = c(2, 2)) を使うとまとめて表示できます）

*  *  *

以下、準備、処理、出力の順に説明します。まず準備からです。2行目と3行目はいつものおまじないです。4行目は毎回のラウンドでコインを投げる回数、5行目はコイン投を繰り返すラウンド数を指定しています。このコードでは、コインを1000回投げる試行を100ラウンド繰り返します。

*  *  *

つづいて処理です。7行目は $n\times r$ 回コインを投げた結果をならべる命令文です。この命令文は前回と同じものです。8行目はコイン投げの結果を r 行 n 列の行列に格納する命令文です。

9行目は行列に格納されたコイン投げの結果を、行ごとに足し上げる命令文です。上で説明したように、apply は、数列に使う関数を行列でも使えるようにする魔法の関数です。第2要素の 1 は、第3要素の cumsum という関数を行に適用するという指定です。（2 にすると、列方向に関数を適用する指定になります。）

9行目までで、それぞれのラウンドの n 回目までに表が出た回数が計算されました。10行目は、9行目で再定義した toss をコインを投げる回数で割っています。10行目で再定義される toss はそれぞれのラウンドの n 回目までに表が出た確率（相対頻度）を表します。

12行目は、それぞれのラウンドで n 回まで投げ終わったときの確率の平均を計算しています。Rでは mean で平均を計算します。13行目は、それぞれのラウンドで n 回まで投げ終わったときの確率の標準偏差を計算しています。Rでは sd で標準偏差を計算します。

行列表記して apply を使うと、計算効率が飛躍的に高まります。

*  *  *

さいごに出力です。15行目は、コイン投げのようすを r ラウンド分まとめてグラフにするとてつもなく便利な命令文です。このコードでは、100回分のグラフ（サンプルパス）を瞬時に描くことができます。上に掲げた左上のグラフがこの1行で描けます。

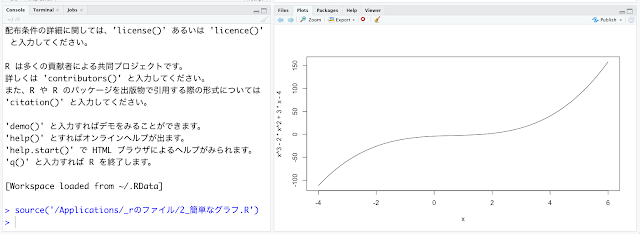
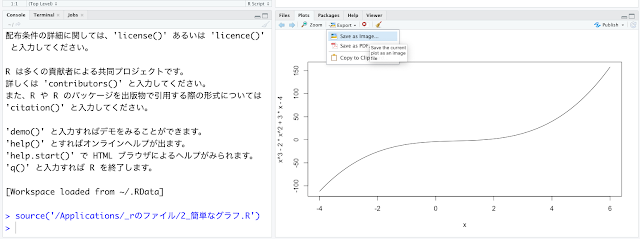
17行目と18行目は、12行目の計算結果（平均の収束）をグラフにする命令文です。上に掲げた右上のグラフに対応します。20行目から22行目は、13行目の計算結果（標準偏差の収束）をグラフにする命令文です。上に掲げた左下のグラフに対応します。

24行目と25行目は、毎回のラウンドでコインを n回投げ終わったときの確率がどのように分布しているか、ヒストグラムで表したものです。点線のグラフは正規分布のグラフです。ヒストグラムは正規分布に近い形をしています。

Rでは、4つのグラフを描くのに10行のコードで済みます。

「まったくおなじ条件で、まったくおなじ実験を、とてもたくさん繰り返す」とき、誤差は平均0、標準偏差 $\sigma/\sqrt{n}$ の正規分布にしたがいます。これを中心極限定理といいます。

中心極限定理はとても難しい統計学の定理です。しかし、今回のコードを実行して得られる4つのグラフから、「まったくおなじ条件で、まったくおなじ実験を、とてもたくさん繰り返す」と、誤差は正規分布することを感じていただけるのではないでしょうか。

*  *  *

補論　中心極限定理を理解するコツ

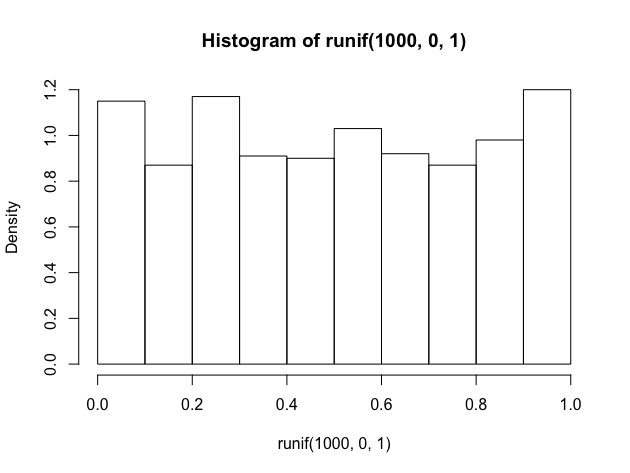
中心極限定理は「どんな分布も、正規分布になる」と軽く説明されることがあります。たとえば、「上段の一様分布が下段の正規分布になる」などと聞いたりします。（そんな説明あり得ないという人は、そう聞こえている、と読み替えてください。）

⇩

このような説明を聞いてはじめ「？？？」だったのですが、真の平均からのずれ（誤差）が正規分布すると知って「なんだ、そいういうことか」と思えました。

コインを2回だけ投げて表が出る確率の誤差より、コインを1000回投げて表が出る確率の誤差が、真の確率50％付近に集まるのは自然なことです。サイコロを2回だけ振って出た目の平均の誤差より、サイコロを1000回振って出た目の平均の誤差が、真の平均3.5近くに集まるのは自然なことです。

考えてみれば当たり前ですが、一様分布が正規分布になるはずありません。正規分布になるのは一様分布ではなく、一様分布からランダムに取り出した値の平均と一様分布の真の平均とのずれ、すなわち誤差です。中心極限定理は誤差のことと強調しないとはじめての人は混乱しますよね…　

Rで大数の法則を感じる（cumsum, sample）

今回は、コインを繰り返し投げて表が出る確率を検証します。わずか10行のコードですので、はじめての人も簡単にできます。

目次

1. コイン投げの確率
2. sample
3. コイン投げの検証

*  *  *

1　コイン投げの確率

コインを投げると表か裏がでます。コインに歪みがなければ、表と裏が出る確率はそれぞれ50％のはずです。

では、歪みがないコインを10回投げたら5回だけ表が出るでしょうか。100回投げたら50回だけ表が出るでしょうか。200回、300回、400回投げつづけたら何回表が出るでしょうか。

本当に投げた回数の50％だけ表が出るの？

今回のコードは、この疑問を検証します。

*  *  *

2　sample

私たちは、おなじことを何度も繰り返すと飽きておざなりになってしまいますが、コンピューターは繰り返し作業がとても得意です。100回、1000回繰り返しても正確無比なままです。私たちが苦手でコンピューターが得意なことは、コンピューターにやってもらいましょう。

Rでは、sample という関数で繰り返し作業を命じます。たとえば、コイン投げを100回繰り返す命令文は次のとおりです。

sample(x=c(0,1), size=100, replace=TRUE)

x=c(0,1) はコイン投げで裏が出ることを数字の0、表が出ることを数字の1と定義しています。0と1が出る確率はそれぞれ50％です。size=100 はコインを100回投げる指定、replace=TRUE は毎回コインを投げ直す指定です。「コインを投げ直す」ことについては、この記事の一番下の補論で説明します。興味のある人はみてください。そこまで興味がない人は、迷わずこのように書きましょう。

*  *  *

3　コイン投げの検証

コイン投げのコードは次のとおりです。コードを入力して実行してみてください。

うまくいけば、右下の領域に次のようなグラフがあらわれます。グラフの形はコイン投げの結果次第ですので実行のたびに変わりますが、似たグラフが出てくるはずです。

横軸はコイン投げの回数です。100は100回投げたことを、700は700回投げたことを表します。私たちがコインを700回投げるのはとても大変ですが、Rなら1秒で終わります。

縦軸は表が出る確率（相対頻度）です。100回くらい投げたとき、表が出たのは50回くらいでした。その後、300回くらいまでのあいだ、表が出る確率は少し低くなりました。300回を超えると、表が出る確率は50％前後で安定しているようにみえます。

300回投げれば150回くらい、400回投げれば200回くらい、…、700回投げれば350回くらい表が出ています。「まったく同じ条件で、まったく同じ実験を、とてもたくさん繰り返す」と、その平均は真の値に近づいてゆきます。これを大数の法則といいます。大数の法則は難しい統計の概念ですが、Rでグラフを書けば、点線にだんだん近づくことだとイメージできます。

*  *  *

以下、準備、処理、出力の順でコードを説明します。まず準備からです。2行目の rm(list=ls()) と3行目の ls() はいつものおまじないです（はじめての人は右のラベルから rm(list=ls()) をクリックしてみてください）。4行目の n=700 はコインを投げる回数です。

*  *  *

つづいて処理です。たった2行です。6行目はコイン投げの結果を記録する命令文です。裏が出たら0、表が出たら1を記録します。コインを700回投げますので、toss には0または1が合わせて700個記録されます。7行目は、6行目の toss に記録されたコイン投げの結果を足し上げる命令文です。たとえば、1回目に裏、2回目に表、3回目に表、4回目に裏が出たとしましょう。これは6行目の toss に次のように記録されます。

toss={0, 1, 1, 0, ...}

これを7行目で足し上げると

toss=cumsum(toss)={0, 1, 2, 2, ...}

となります。このように toss を定義し直します。たった2行ですが、多くの作業が含まれています。

*  *  *

さいごに出力です。これもたった2行です。9行目は折れ線グラフを書く命令文です。(1:n) は 1から n まで整数をならべる命令文です。7行目で定義した toss と (1:n) を示すと

toss={0, 1, 2, 2, ...}

(1:n)={1, 2, 3, 4, ...}

toss/(1:n) は上段の数を下段の数でそれぞれ割る命令文ですので

toss/(1:n)={0, 1/2, 2/3, 2/4, ...}

となります。2つめと4つめの値は理論上の確率50%と等しいです。9行目だけで、コインを投げる回数それぞれで表が出る確率を計算して、結果をグラフにすることができます。

10行目は理論上の確率50％（0.5）を描き加える命令文です。lty=3 は、グラフを点線で描く指定です。

*  *  *

補論　replace=TRUE について

6行目の命令文にある replace=TRUE は毎回コインを投げ直す指定です。高校の確率の授業で学んだ「袋から白玉、赤玉を取り出す」試行では、TRUE は袋から取り出した玉を袋に戻すことにあたります。このとき、白玉を取り出す確率は毎回変わりません。

これを replace=False とすると、取り出した玉を袋に戻さないことになります。取り出すたびに袋に残る玉は減りますので、白玉を取り出す確率は変わります。コイン投げであれば、表が出たら、残りは裏しか出ようがありませんので、裏が出る確率は100％になってしまいます（同様に、裏が出た後表が出る確率も100％になります）。そして、表と裏（あるいは裏と表）が出たら、ほかに出るものがないのでプログラムは止まってしまいます。私たちはコイン投げを何度も繰り返したいので、replace=TRUE と指定します。

Rでテイラー展開する (function、plot、legend)

今回は関数を近似するテイラー展開を紹介します。テイラー展開をまったく知らない人も、Rを使えばイメージできるようになります。やってみましょう。

目次

1. 指数関数のテイラー展開
2. function、plot、legend
3. テイラー展開による関数の近似

*  *  *

1　指数関数のテイラー展開

前回に引き続き、ネイピア数 $e$ を底とする指数関数を例に考えます。

$$y=e^x$$

この関数を0のまわりでテイラー展開すると（式の導出はこの記事の補論を参照してください）

$$e^x=1+\frac{1}{1!}x^1+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+\frac{1}{5!}x^5+...$$

となります。式中の！は階乗です。たとえば、$3!=3\times 2\times 1=6$ です。階乗の計算をして式をきれいにすると

$$e^x=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\frac{1}{24}x^4+\frac{1}{120}x^5+...$$

前回のマクローリン級数は関数の値を近似するためのものでしたが、今回のテイラー級数は関数を近似するためのもです。指数関数 $y=e^x$ が右辺の多項式によって表現されるというのがテイラー展開の意味するところです。

*  *  *

2　function、plot、legend

複雑なグラフをきれいに描くとき便利な関数を紹介します。function はグラフを描く関数を定義するためのものです。たとえば、$y=e^x$ という関数を定義するときには

y <- function(x){exp(x)}

と書きます。function(x) は y が x の関数であることを表しています。{exp(x)} は関数の姿が $e^x$ であることを表しています。

function で定義した関数をグラフにするとき plot を使います。この関数は前回も使いましたが、今回はグラフを点線にしたり、グラフに色をつけたり、複数のグラフを重ねたりといった少し高度な使い方をします。

下の2行のコードを例に説明します。1行目は function で定義した y という関数を $-3\leq x\leq 3$ の範囲でグラフにする命令文です。plot の第4要素 type="l" は折れ線グラフで表す指定です（l はエルです）。2行目は function で定義した d1y という関数を $-3\leq x\leq3$ の範囲でグラフにする命令文です。第4要素以降はグラフの細かい設定です。lty=2 はグラフを点線にする指定、col=2 はグラフの色を2番（赤）にする指定、add=TRUE は2行目のグラフを1行目のグラフに重ねて表示する指定です。

plot(y, -3, 3, type="l")
plot(d1y, -3, 3, lty=2, col=2, add=TRUE)

legend は描いたグラフに凡例（変数一覧）をつけるためのものです。下の2行のコードを例に説明します。1行目は変数の名前を定義する命令文です。c() を使って、凡例に表示する2つの変数の名前 "e^x" と "1st" をならべています。文字をならべるときは要素を "" で囲みます。2行目はグラフに凡例をつける命令文です。legend() の中は凡例の細かい設定です。"topleft" は凡例をグラフの左上におく指定、legend=lc は1行目で定義した2つの変数の名前を表示する指定、lty=c(1,2) は e^x を実線、1st を点線にする指定、col=c(1,2) は e^x を黒、1st を赤で表示する指定です。

lc<-c("e^x", "1st")
legend("topleft", legend=lc, lty=c(1,2), col=c(1,2))

グラフについて詳細は下のリンク先をご覧ください。英語で申し訳ないです。日本語での説明はグーグル検索をご利用ください。
https://cran.r-project.org/doc/manuals/r-release/R-intro.html#High_002dlevel-plotting-commands

*  *  *

3　テイラー展開による関数の近似

ネイピア数を底とする指数関数はテイラー展開で近似できるか、Rで検証します。下の画像をクリックすると大きくなりますので、それをみてコードを入力しましょう。入力を終えましたら左上の ☑️ を入れてから💾 を押してみましょう。（「➡️Run」を押すとうまくいかないことがあるようです…　原因がわかる人がいましたら、教えてください 🙇‍♂️）

少し長いコードですが、構造は比較的シンプルですのでなんとか頑張りましょう。うまくいけば、右下にグラフが2つ出てきます。重なっていますので ⬅️➡️ をクリックしてみてください。

*  *  *

以下、準備、処理、出力の順でコードを説明します。このコードは準備と処理が一体化していますので、まとめて説明します。2行目と3行目はいつものおまじないです。5行目から9行目までは式の定義です。式とコードを対応させると次のようになります。

指数関数（$e^x$）　exp(x)

テイラー展開
〜$x^1$の項（$1+x$）　1+x
〜$x^2$の項（$1+x+\frac{x^2}{2!}$）　1+x+x^2/2
〜$x^3$の項（$1+x+\frac{x^2}{2!}+\frac{x^3}{3!}$）　1+x+x^2/2+x^3/6
〜$x^5$の項（$1+x+...+\frac{x^5}{5!}$）　1+x+x^2/2+x^3/6+x^4/24+x^5/120

*  *  *

出力では、描画を2度くりかえします。それぞれの命令文を分けて説明します。11行目から14行目はグラフの描画です。11行目は指数関数 $y=e^x$ 、12行目はテイラー展開の $x$ を含む項まで、13行目はテイラー展開の $x^2$ を含む項までのグラフです。これらのグラフを1枚の図にまとめて表示するため、plot 関数の中で add=TRUE と指定します。

14行目は $x=0$ の点線を書き加える命令文です。この点線は、指数関数を0のまわりでテイラー展開していることを表します。テイラー展開は、0のまわりで指数関数をよく近似します。

16行目と17行目は凡例を図示する命令文です。16行目は、図示する3つのグラフの名前をそれぞれ e^x、1st、2nd と指定しています。17行目は、グラフの名前を取り込んで、左上に凡例を表示する命令文です。さいごの要素 bty="n" は、凡例に枠をつけないことを指定しています。上に掲げた上段の図はこのように描きます。








図をみると、2nd の緑のグラフは x がマイナスの領域で上に跳ねてしまっています。これは $x^2$ が左右対称のグラフであるためです。同様に、$x^4$、$x^6$ など、べき指数が偶数のとき、マイナスの領域でグラフが跳ね上がります。

ここでは指数関数の近似を考えていますので、べき指数が奇数の項までのときだけグラフにしてみましょう。下段の図はそのようなグラフです。コードは次のとおりです。命令文の大半は1つめの図のものとおなじですので説明を割愛します。違いはべき指数が奇数となる項までのテイラー級数だけグラフにしている点です。









下段の図をみると、$x^5$ の項までのテイラー展開は、0のまわりで指数関数をうまく近似しています。これがテイラー展開の妙味です。

*  *  *

補論　テイラー展開とマクローリン級数

この補論は込み入っています。興味のある人だけみてください。テイラー展開とは、関数のおおよそのふるまいをみるためのものです。式にするととてもいかめしいのですが、$a$ のまわりで展開すると

$$f(x)=f(a)+\frac{f'(a)}{1!}(x-a)^1+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+...$$

となります。ここで $f'(a)$、$f''(a)$、$f'''(a)$ は、それぞれ関数を1回、2回、3回微分したものです。この式のおおまかな意味は、$x$ の値が $a$ にとても近いとき、関数のふるまいは微分を繰り返して足したもので表せるということです。

*  *  *

ネイピア数 $e$ を底とする指数関数 $f(x)=e^x$ を例に考えましょう。ネイピア数と指数関数については姉妹ブログ『文系の "だいたい" 数学』をご参照ください。

https://easy-suugaku.blogspot.com/2020/04/blog-post_4.html

https://easy-suugaku.blogspot.com/2020/04/e.html

$f(x)=e^x$ は、何回微分してもその導関数が $e^x$ になります。つまり

$$f(x)=e^x　f'(x)=e^x　f''(x)=e^x　f'''(x)=e^x$$

$e^x$ の $x$ に $a$ を代入すると

$$f(a)=f'(a)=f''(a)=f'''(a)=e^a$$

さらに、$a=0$ を代入すると

$$f(0)=f'(0)=f''(0)=f'''(0)=e^0=1$$

この結果をテイラー展開の各項の分子に代入すると（$a=0$）

$$e^x=1+\frac{1}{1!}x^1+\frac{1}{2!}x^2+\frac{1}{3!}x^3+...$$

これが今回使ったネイピア数を底とする指数関数をテイラー展開して得られるテイラー級数です。この式に $x=1$ を代入すると

$$e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...$$

となります。これが前回使ったマクローリン級数です。指数関数が級数で表されるのはとても不思議ですね…　（nが無限大に近づくときのふるまい（収束）などについては難しすぎますので説明を割愛します。数学の本をご参照ください。）

Rでマクローリン展開する ((1:n), cumprod, plot)

今回は、関数の値を近似するマクローリン展開を紹介します。マクローリン展開をまったく知らない人も、Rを使えばイメージできるようになります。やってみましょう。

目次

1. 指数関数のマクローリン展開
2. (1:n) 、cumprod
3. マクローリン級数による値の近似

*  *  *

1　指数関数のマクローリン展開

指数関数とは、$y=2^x$ のように、$x$ が（べき）指数にある関数です。ネイピア数 $e$ を底とする指数関数は

$$y=e^x$$

と書けます。この関数をマクローリン展開すると下式のようになります。（導出の詳細は次回の補論で説明する予定です。）

$$e^x=1+\frac{1}{1!}x^1+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+\frac{1}{5!}x^5+...$$

式中の！は階乗です。たとえば、$3!=3\times 2\times 1=6$ です。階乗の計算をして式をきれいにすると

$$e^x=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\frac{1}{24}x^4+\frac{1}{120}x^5+...$$

はじめてみる人は「なにこれ？」という感じだと思います。この多項式は関数の値を近似します。$x=1$ なら、左辺は $e^1=e$ となります。$e$ は2.71828くらいの値をとるネイピア数です。右辺の多項式がこの値とおなじになるというのが、マクローリン級数の意味するところです。

*  *  *

2　(1:n) 、cumprod

コードを効率よく書き、短時間で実行するのに便利なのがベクトル型の命令文です。今回新たに登場するのは (1:n) と cumprod です。

(1:n) は、1から n まで整数を並べる命令文です（n は j や k などほかの文字でも構いません）。たとえば、n=5 のとき (1:n) は

(1:5)=1, 2, 3, 4, 5

となります。cumprod  は並んだ数を順に掛ける関数です。たとえば

 cumprod((1:5))

であれば、{1,2,3,4,5} という数の並びを順に掛けます。すなわち

1, 1*2, 1*2*3, 1*2*3*4, 1*2*3*4*5

それぞれ計算すると

cumprod((1:5))=1, 2, 6, 24, 120

となります。興味深いことに、cumprod((1:5)) は、1から5の階乗を並べたものになります。すなわち

cumprod((1:5))=1!, 2!, 3!, 4!, 5!

ベクトル型の命令文は、コードをすっきりさせます。

*  *  *

3　マクローリン級数による値の近似

ネイピア数はマクローリン級数で近似できるか、Rで検証します。下の画像をクリックするとコードが大きく表示されますので、それをみて入力してください。入力が終わりましたら「➡️Run」を押してみましょう。

うまくいけば、左下と右下に次のように表示されます。










左に示されている [1] 2.731266058e-08 はネイピア数とマクローリン級数の値の差です。指数で $2.73...\times 10^{-8}$ と表されます。これは、差がほとんどないことを意味します。下のグラフは、右のグラフを拡大したものです。マクローリン級数の値を示す○は、級数の項が増えるにしたがい、ネイピア数の値を表す点線に近づきます。

*  *  *

以下、準備、処理、出力の順にコードを説明します。まず準備からです。2行目と3行目はいつものおまじないです。Rのコードはこの2行からはじめましょう。

5行目の x=1 は x の値を1に指定しています。このコードでは、x の値が1でない場合についても検証できます。6行目の n=10 は、マクローリン級数の項数の上限を指定しています。n=10 のとき x を含む10の項と第1項の1、あわせて11項を上限として級数を計算します。

*  *  *

つづいて処理です。8行目の vx は多項式の分子をまとめて計算するためのものです。n が5なら、(1:n)=1,2,3,4,5 ですので

vx=x^1, x^2, x^3, x^4, x^5

となります。ここでは n=10 ですので、x^10 まで数がならびます。9行目の vf は多項式の分母をまとめて計算するためのものです。上で説明したように、n が5なら

cumprod((1:5))=1!, 2!, 3!, 4!, 5!

となります。ここでは n=10 ですので、10! まで数がならびます。10行目の mac は、マクローリン級数の第2項から第11項を表しています。vx を vf で要素ごとに割り算しますので

mac=x^1/1!, x^2/2!, x^3/3!, x^4/4!, x^5/5!, ...

となります。11行目は、mac の先頭に1をつけてできた数列の要素を順に足し上げて mac を再定義しています。言葉で説明するより数列を示した方が理解しやすいかもしれません。次のような数列が11項までつづきます。

mac
=1, 1+x^1/1!, 1+x^1/1!+x^2/2!, 1+x^1/1!+x^2/2!+x^3/3!, ...

わずか4行ですが、たくさんの工程がたたみ込まれています。

*  *  *

さいごに出力です。前々回、curve というグラフを描く関数を紹介しました。今回は plot を使います。13行目にある plot の第1要素 (0:n) は横軸の数字です。0から10までをとります。第2要素 mac は、マクローリン級数の数列です。14行目の abline は、級数の計算結果のグラフに、ネイピア数の値（h=exp(x)）を点線で（lty=3）描き加える命令文です（ここでは x=1 です）。

15行目は、ネイピア数と第11項までのマクローリン級数の値の差を計算して印字する命令文です。先ほどみましたように、差はほぼ0です。

*  *  *

わずか15行のコードですが、説明すると盛りだくさんですね…　Rはそれだけ効率のよい言語だともいえます。効率のよいコードがうまく動くと爽快です。是非トライしてみてください。

Rで微分する (expression、D、print)

今回は微分です。「プログラミングで微分ができるの？」と思いますが、Rはとても優秀な言語ですので、簡単にできます。


目次

1. 微分とは
2. expression と D
3. 微分

*  *  *

1　微分とは

$x$ がわずかに動いたとき、関数の値はどれくらい動くか調べる作業を微分といいます。ここでは微分の定義ではなく、微分のやり方をおさらいします。微分は3段階の手順でできます。

a　$x$ の肩に乗っている（べき）指数という重荷をおろす
b　重荷を1回おろしたことを記録する
c　式をきれいにする

くわしいことは姉妹ブログ『文系の "だいたい" 数学』をご覧ください。
https://easy-suugaku.blogspot.com/2020/04/blog-post_16.html

*  *  *

2　expression と D

Rで関数を微分するとき、関数を定義して、それを微分するという2段階のコードを書きます。expression は関数を定義するのに使います。たとえば、$f(x)=x+2$ という関数を定義するとき

f <- expression(x+2)  

と書きます。f は定義する関数の名前、<- は「…と定義する」という意味の記号です。定義した関数を微分するとき、D を使います。たとえば、定義した関数 f を微分するとき

D(f, "x")

と書きます。() の中の第1要素は定義した関数を、第2要素は関数を x について微分することを表します。

*  *  *

3　微分

関数を微分するRのコードは次のとおりです。はじめての人にわかりやすくするために、少し冗長に書きました。画像をクリックすると大きくなりますので、それをみてコードを入力しましょう。入力できたら「➡️Run」を押してみてください。










うまくいけば、左下の領域に次のような結果が出てきます。











Rは、微分の3段階のうち、aとｂの2段階をやってくれるようです。さいごのｃ（式をきれいにする）は、Rの結果をもとに私たちがやることになりそうです。もし、式をきれいにするコードをご存知の方がいましたら教えていただけると嬉しいです。 🙇‍♂️

*  *  *

以下、準備、処理、出力の順にコードを説明します。まず準備からです。このコードでははじめの10行にあたります。2行目と3行目はいつものおまじないですので説明を省略します。はじめてでよくわからないという人は、ブログ右のラベルから rm(list=ls()) をクリックして関連記事をみてください。

5行目から10行目は、関数を定義しています。上から1次関数、2次関数、3次関数、2を底とする指数関数、2を底とする対数関数、ルート関数です。前回作図したグラフとおなじ式です。関数の記号として i を使わないのは、Rでは虚数単位を i で表すためです。10行目のアルファベット記号はエルです。

*  *  *

つづいて処理です。このコードでは12行目から17行目にあたります。上で定義した式を x で微分して、結果を df、dg、dh、dj、dk、dl に格納します。

*  *  *

さいごに出力です。このコードでは19行目にあたります。c() は、要素をならべて表示する関数です。その外側にある print() は、ならべた要素を印字する関数です。たった1行で、微分の結果をならべて印字させることができます。Rはとても効率的な言語です。

*  *  *

今回のコードは20行ですが、大部分繰り返しですので、難しくはなかったと思います。少しずつ慣れていきましょう。

Rでグラフを描く (curve)

今回は、グラフを描く最もやさしい方法を紹介します。はじめての人でもすぐできます。是非ご覧ください。

目次

1. curve
2. ｎ次関数のグラフ
3. その他のグラフ

*  *  *

1　curve

Rには、グラフを描く関数がいくつもあります。そのうち最もやさしいのは curve だと思います。たとえば、$x$ の範囲を $-4$ から $6$ と指定して1次関数 $y=x+2$ のグラフを描くには

curve（x+2, -4, 6）

と入力します。curve の () の中は、左から順に関数、$x$ の最小値、$x$ の最大値です。$x$ の最小値と最大値は自由に決められます（0から100までなど）。

*  *  *

グラフを描くコードは次のとおりです。コードが書けたら「➡️Run」を押してみてください。たった10行でいろいろなグラフが描けます。

2行目の rm(list=ls()) と3行目の ls() については、前回の記事をご覧ください。

*  *  *

2　ｎ次関数のグラフ

5行目から7行目までは、ｎ次関数のグラフを描く命令文です。関数とコードを対応させると次のようになります。

1次関数（$y=x+2$）　　x+2
2次関数（$y=-x^2+2x-3$）　　-x^2+2*x-3
3次関数（$y=x^3-2x^2+3x-4$）　　x^3-2*x^2+3*x-4

関数のグラフは右下の領域に重なっています。上段の図では1次関数が表示されていますが、⬅️➡️ のボタン（図が小さくてみづらいですが ）を押すと2次関数、3次関数のグラフがあらわれます。






























グラフはPNGファイルとして保存できます。「Export」をクリックして、「Save as Image」をクリックすると










こんな画面になります。「Directory」で保存したいフォルダを選んで保存しましょう（この図ではデスクトップを指定しています）。



















少々殺風景なグラフですが、横軸と縦軸に名前がついていますし、目盛りもありますので必要は満たしていると思います。エクセルより簡単に描けるのは大きなメリットです。

*  *  *

3　その他のグラフ

8行目から10行目は順に指数関数、対数関数、ルート関数のグラフを描く命令文です。関数とコードを対応させると次のようになります。

指数関数（$y=2^x$）　　curve(2^x, -4, 6)
対数関数（$y=log_2x$）　　curve(log2(x), 0.001, 6)
ルート関数（$y=3\sqrt{x+2}$）　　curve(3*sqrt(x+2), -2, 6)

指定する $x$ の範囲を関数によって変えています。対数関数は $x$ がプラスでないとき値が定義されませんので、$x$ を0.001以上としました。ルート関数はルートの中がマイナスのとき実数でなくなってしまうので、$x$ を $-2$ 以上としました。それぞれの関数のグラフは次のようになります。
























対数関数とルート関数は、関数の値が小さい領域で滑らかさが失われカクカクしていますが、これは受け入れるしかなさそうです。グラフのデザインにこだわりたい人は、より複雑なコードを書くか、他の描画ソフトを使うことになりそうです。

それぞれのグラフを描くコードはたった1行です。是非気楽にやってみてください。「あっ、できた」という小さな達成感を積み上げましょう。

Rでかんたんな計算をする (四則演算、指数対数など)

前回、RとRStudioのセットアップをしました。今回からプログラミングに入ります。はじめですので、ごく簡単な計算をします。

目次

1. 四則演算の記号
2. 四則演算
3. 指数対数、ルート、e、π

*  *  *

1　四則演算の記号

四則演算とは＋、ー、×、÷の基礎的な計算です。Rでは、次のような記号で計算します。右側に読み方とキーボードの位置をひらがなの配置で示しています。

足し算　+　　プラス記号：ひらがなの「れ」のところ

引き算　-　　マイナス記号：ひらがなの「ほ」のところ

掛け算　*　　アスタリスク：ひらがなの「け」のところ

割り算　/　　スラッシュ：ひらがなの「め」のところ

*  *  *

2　四則演算

四則演算のコードは次のとおりです。RStudioを開いて、左上のところに、同じように入力してみましょう。スペースや改行も含め、すべて半角英数で入力しましょう。（このコードでは、ならべて表示 だけ全角です。）また、Rは大文字と小文字を別物と判断しますので、気をつけましょう。

2行目の rm(list=ls()) と3行目の ls() はおまじないだと思って書いておきましょう。2行目は変数をリセットする命令文です。これを書かないと、他のコードに書いてある変数がこのコードに入り込んで邪魔してしまうようです。それを避けるために、変数をいったんリセットします。3行目はリセットしたことを確かめるためのものです。Rのコードはこの2行からはじめましょう。

5行目から8行目は四則演算です。上から順に足し算、引き算、掛け算、割り算です。計算結果はそれぞれ a,b,d,e に格納されます。a,b,c,d としなかったのは、10行目にある関数 c() との混同を避けるためです。c() は、数字などをひとまとめ（ベクトル）にする関数です。print() は、c() に納めた4つの計算結果を表示させる関数です。

コードを書いたら、右上の「➡️RUN」を押してみましょう。左下の領域に次のような計算結果が表示されます。

5.0000000 -1.0000000  6.0000000  0.6666667

これらは順に、 a,b,d,e の計算結果です。e の値は $\frac{2}{3}$ ですので、割り切れません。最後の桁で四捨五入した結果が表示されます。

*  *  *

3　指数対数、ルート、e、π

そのほかの基礎的な計算もやってみましょう。指数、対数、ルートなどの記号は、次のとおりです。右側に読み方とキーボードの位置、表記の仕方を添えました。

指数　　^         　　ハット：ひらがなの「へ」のところ

対数　　log(a,b)  　　ログ：aは真数、ｂは対数の底
ルート　sqrt()　　　ルート

e    　　exp(1)    　　エクスポネンシャル：カッコ内は数字の1です

pi　   　pi.        パイ

*  *  *

これらを計算するコードは次のとおりです。RStudioを開いて、左上のところに、同じように入力してみましょう。スペースや改行も含め、すべて半角英数で入力しましょう。

pi は値が定まっていますので、直接 c() の中に書いています。コードを書いたら、右上の「➡️Run」を押してみましょう。左下の領域に次のような計算結果が表示されます。

8.000000 3.000000 1.414214 2.718282 3.141593

です。a は $2^3$ ですので8です。b は $log_28$、つまり「2を何乗すれば8になりますか」という問いですから、3です。d は$\sqrt{2}$、e はネイピア数、pi は円周率ですから割り切れません。それで、表示される最後の桁は四捨五入した値になります。

これくらいの計算ができれば、とりあえず大丈夫です。ここで紹介していない計算は、必要なとき学ぶ感じでいいと思います。

*  *  *

* この記事は2022/9/20にアップデートしました。

RとRStudioの導入 (RStudio Cloud)

今回はRというプログラミング言語を使うための環境設定についてです。お使いのパソコンによってやりかたが少しずつ異なりますが、大筋は同じ手順だと思います。ここでは、iMacへの導入を例に説明します。Windowsをお使いの人は、参考までご覧いただければと思います。

（注意！　ほとんどの人にとって、この作業が一番難しいと思います。プログラムを書くより難しいかもしれません。不安な人は、近くにいるパソコンが得意な人に聞いてください。YouTubeにもインストールの仕方の動画があるようですので検索してみてください。また、万が一、この段階の操作でパソコンが故障したりしましても、一切責任を取れません。自己責任で作業していただきますようお願いいたします。通常の作業でパソコンが故障するようなことはないと思いますが、免責事項として明記しておきます。）

目次

1. Rのダウンロード
2. RStudioのダウンロード
3. 動作確認
4. RStudio Cloudのご紹介

*  *  *

1　Rのダウンロード

Rは、インターネットからダウンロードして使います。まず、ダウンロードするパソコンを用意しましょう。パソコンが用意できたら、こちらへアクセスしましょう。こんな画面になるはずです。

（https://cran.ism.ac.jp/より画像を取得）

ほどんどの人はWindowsかiMacのパソコンを使っていると思います。ご自身のパソコンがどちらか確認してください。Windowsであれば「R for Windows」を、iMacであれば「R for (Mac) OS X」をクリックします。

ここでは、Macをクリックします。クリックするとこんな感じの英文が出てきます。英文はわからなくても大丈夫です（読んだ方がいいと思いますが…）。古めのmacを使っている人は、左にある青いところ、R-4.2.1.pkgをクリックしましょう。新しめのmac（AppleシリコンM1/M2チップ搭載のものなど）を使っている人は、R-4.2.1-arm64.pkgをクリックしましょう。「4.2.1.」というのはバージョンを表す数字です。時が経つとバージョンが新しくなり、数字は変わると思いますが、あまり気にしなくて大丈夫です。（この情報は2022年9月中旬の情報です。）

（https://cran.ism.ac.jp/より画像を取得）

私はデスクトップにダウンロードしました。ダウンロードが終わると、次のようなマークがデスクトップにあらわれます。

みなさんのパソコンの設定次第では、デスクトップではなく「ダウンロード」というフォルダに入っているかもしれません。探してみてください。

このマークをクリックするとインストール（Rをパソコンに導入する作業）がはじまります。何回か「続ける」ボタンを押す作業がありますが、ほぼ自動的に作業が進みます。作業が終わると「✅インストールが完了しました」というメッセージが出ます。

*  *  *

2　RStudioのダウンロード

つづいて、R Studioというものを導入します。これは、Rのプログラムコードを書くのに使います。こちらにアクセスしてください。

（https://rstudio.com/products/rstudio/download/より画像を取得）

ありがたいことに、一番左にFreeの文字がみえます。ここでは、個人で楽しむことを前提にしていますので、Freeの下にある「DOWNLOAD」をクリックします。下のような画面が出てきますので、左下にある🍏のところをクリックしましょう。ダウンロードがはじまります。

（https://rstudio.com/products/rstudio/download/#downloadから画像を取得）

ダウンロードが終わると、次のようなマークがあらわれます。

マークをクリックするとインストールがはじまります。インストールが終わると「アプリケーション」というフォルダに「RStudio」というものが登場します。これをデスクトップに移動させます。RStudioのマークはこんな感じです（バージョンによって少し違うかもしれません）。

このマークをクリックすると、ソフトが次のように立ち上がります。（何か追加のインストールを求められることもあるようですが、適宜対応をしてください。）イメージを持っていただくために画像を大きく表示します。

私はRの専門家ではないので、使う人の立場でこの画面を説明します。画面が4分割されていますね。それぞれの役割は次のとおりです。

左上　プログラムコードを書くところ

左下　プログラムがうまく動いているか確認するところ

　　　（エラーメッセージはここに出ます）

右下　プログラムで描くグラフなどが出るところ

右上　プログラムで使う変数などが表示されるところ

左上に書いて、左下でチェックし、右下で結果を見る感じです。なんとかRStudioを動かせるところまで環境を整えてみてください。環境を整えられる人は、プログラムも問題なく書けると思います。

*  *  *

3　動作確認

さいごに、ちゃんと動くか確認しましょう。すごく簡単なコードを書きます。RStudioを立ち上げたら、名前をつけてファイルを保存します。

はじめですので、「動作確認」という名前にして保存しました。Rのファイルをたくさん作りたい人は、専用のフォルダを作ってそこに保存することをお勧めします。

ファイルの保存が終わりましたら、コードを書きます。動作確認ですので簡単なコードにしましょう。1+2 と書いてください。必ず半角英数で入力しましょう。Rは全角文字を読むことができません。入力ができましたら右上の「➡️Run」をクリックしてください。









左下に次のように表示されたら成功です。これは「1+2をしてください」とRに命じて、Rがそれを理解して「答えは3です」と回答したことを表しています。






これで準備ができました。次回から、少しずつコードを書いていきましょう。

*  *  *

4　RStudio Cloudのご紹介

上の手順でインストールができなかった人、Rがどういうものか確かめてからインストールしたい人、iPadなどを使っていてハード側の制約が大きい人に、RStudio Cloudを紹介します。デスクトップ版のRStudioと同じ作業ができるようです。（そのように思われます。）

下のアドレスにアクセスしましょう。
https://rstudio.cloud/

（https://rstudio.cloud/ から画像を取得）

Get StartedをクリックするとEmailアドレス、パスワード、名前（First NameとLast Name）を入力します。名前はニックネームで大丈夫です。入力が終わりましたらSing upをクリックしましょう。

（https://rstudio.cloud/ から画像を取得）

Sign upすると、次のような画面になります。画像が小さくてみづらいですが、New Projectをクリックします。

（https://rstudio.cloud/ から画像を取得）

立ち上がるまで少し時間がかかりますが、デスクトップ版のRStudioと同じ画面になります。左上に1+2と入力して、「➡️Run」をクリックしてみてください。左下に「3」がでたら、うまく動いていると思います。このブログで紹介するコードは長くても30行くらいですので、クラウド版を使われてもよいかと思います。

（https://rstudio.cloud/ から画像を取得）

これで準備が整いました。プログラミングを楽しみましょう！　

*  *  *

* R言語を開発した人の記事がありましたので紹介します。

https://business.nikkei.com/atcl/report/16/122700258/010900004/

* この記事は2022/9/18にアップデートしました。