目次
- curve
- n次関数のグラフ
- その他のグラフ
* * *
1 curve
Rには、グラフを描く関数がいくつもあります。そのうち最もやさしいのは curve だと思います。たとえば、$x$ の範囲を $-4$ から $6$ と指定して1次関数 $y=x+2$ のグラフを描くには
curve(x+2, -4, 6)
と入力します。curve の () の中は、左から順に関数、$x$ の最小値、$x$ の最大値です。$x$ の最小値と最大値は自由に決められます(0から100までなど)。
* * *
グラフを描くコードは次のとおりです。コードが書けたら「➡️Run」を押してみてください。たった10行でいろいろなグラフが描けます。
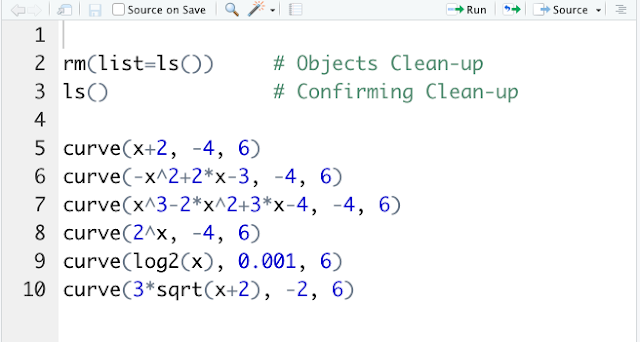
* * *
2 n次関数のグラフ
5行目から7行目までは、n次関数のグラフを描く命令文です。関数とコードを対応させると次のようになります。
1次関数($y=x+2$) x+2
2次関数($y=-x^2+2x-3$) -x^2+2*x-3
3次関数($y=x^3-2x^2+3x-4$) x^3-2*x^2+3*x-4
関数のグラフは右下の領域に重なっています。上段の図では1次関数が表示されていますが、⬅️➡️ のボタン(図が小さくてみづらいですが )を押すと2次関数、3次関数のグラフがあらわれます。

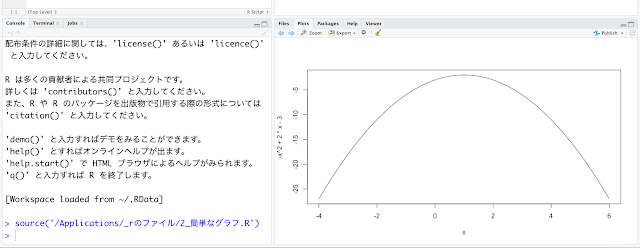
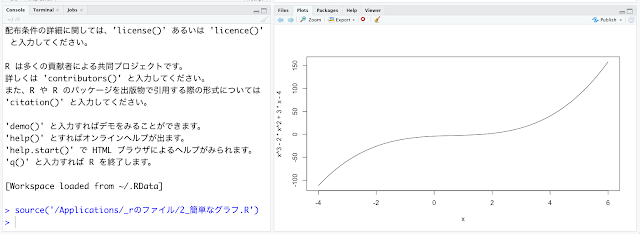
グラフはPNGファイルとして保存できます。「Export」をクリックして、「Save as Image」をクリックすると
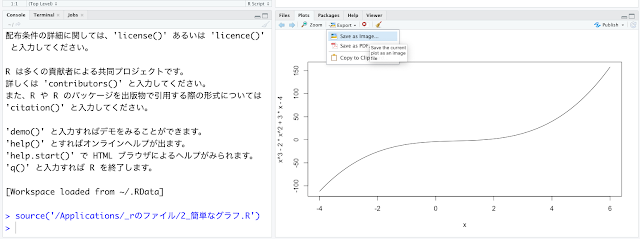
こんな画面になります。「Directory」で保存したいフォルダを選んで保存しましょう(この図ではデスクトップを指定しています)。
少々殺風景なグラフですが、横軸と縦軸に名前がついていますし、目盛りもありますので必要は満たしていると思います。エクセルより簡単に描けるのは大きなメリットです。
* * *
3 その他のグラフ
8行目から10行目は順に指数関数、対数関数、ルート関数のグラフを描く命令文です。関数とコードを対応させると次のようになります。
指数関数($y=2^x$) curve(2^x, -4, 6)
対数関数($y=log_2x$) curve(log2(x), 0.001, 6)
ルート関数($y=3\sqrt{x+2}$) curve(3*sqrt(x+2), -2, 6)
指定する $x$ の範囲を関数によって変えています。対数関数は $x$ がプラスでないとき値が定義されませんので、$x$ を0.001以上としました。ルート関数はルートの中がマイナスのとき実数でなくなってしまうので、$x$ を $-2$ 以上としました。それぞれの関数のグラフは次のようになります。
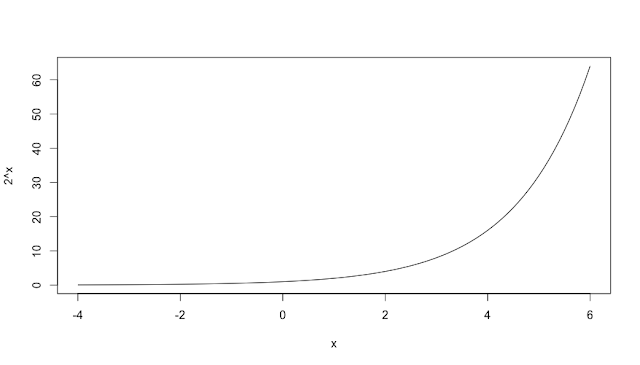
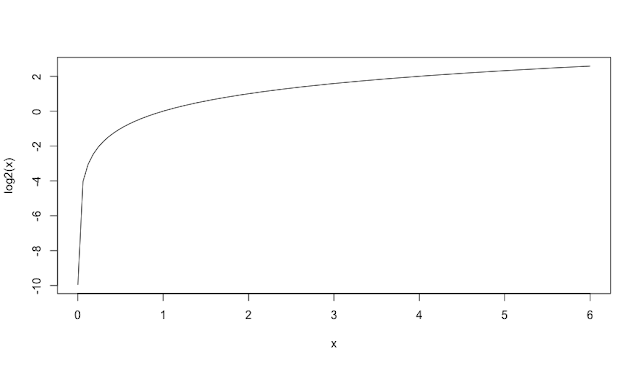
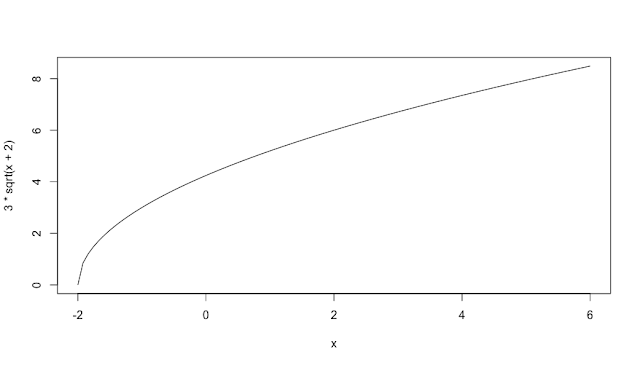
対数関数とルート関数は、関数の値が小さい領域で滑らかさが失われカクカクしていますが、これは受け入れるしかなさそうです。グラフのデザインにこだわりたい人は、より複雑なコードを書くか、他の描画ソフトを使うことになりそうです。
それぞれのグラフを描くコードはたった1行です。是非気楽にやってみてください。「あっ、できた」という小さな達成感を積み上げましょう。